Kaip dvejetą pastatyti per vidurį, vienetą – priekyje, o trejetą – gale? Rikiavimo algoritmai.
 Ilgokai jau čia nerašiau. Kodėl? Pirma, tai dėl to, nes nelabai turėjau laiko visą mėnesį, antra, nes paprasčiausiai neturėjau idėjų, apie ką galėčiau parašyti. Tarp kitko, atsiprašau už tai, kad lapkričio 16-17 dienomis kažkuriuo metu tinklaraštis nebuvo pasiekiamas – EuroVPS perkėlė mane į kitą serverį, pažadėjo geresnę kokybę – žiūrėsim, kaip čia bus.
Ilgokai jau čia nerašiau. Kodėl? Pirma, tai dėl to, nes nelabai turėjau laiko visą mėnesį, antra, nes paprasčiausiai neturėjau idėjų, apie ką galėčiau parašyti. Tarp kitko, atsiprašau už tai, kad lapkričio 16-17 dienomis kažkuriuo metu tinklaraštis nebuvo pasiekiamas – EuroVPS perkėlė mane į kitą serverį, pažadėjo geresnę kokybę – žiūrėsim, kaip čia bus. ![]()
Taigi, prie reikalo: turbūt visi pastebi, kad informacija kažkokiose programose, internetiniuose puslapiuose dažnai būna surikiuota tarkim pagal datą, abėcėlę, skaičių eilės tvarką ar pan. Kaip programuotojai sugeba surikiuoti (surūšiuoti) duomenis eilės tvarka? Na, tam yra keletas algoritmų, dažniau naudojamus čia ir pamėginsiu apžvelgti.
 Pirmas ir vienas iš paprasčiausių rikiavimo algoritmų yra vadinamas „Selection sort“ (išrinkimo algoritmas). Algoritmo veikimo principas labai paprastas: visas duomenų masyvas yra „skenuojamas“ ir ieškoma pačio mažiausio elemento, tada tas elementas yra nukeliamas į masyvo pradžią (jeigu reikia, kad duomenys būtų surikiuoti nuo mažiausio iki didžiausio). Vėliau ciklas kartojamas, tik šįkart netikrinant pirmojo masyvo elemento. Iš krūvos likusių elementų yra išrenkamas mažiausias ir jis jau yra statomas į antrąją masyvo vietą. Vieno ciklo („skenavimo“) metu gali būti perkeliamas tik vienas elementas, todėl šis algoritmas yra ganėtinai lėtas, jeigu duomenų kiekiai yra dideli. Manau iš iliustracijos suprasti bus šiek tiek lengviau.
Pirmas ir vienas iš paprasčiausių rikiavimo algoritmų yra vadinamas „Selection sort“ (išrinkimo algoritmas). Algoritmo veikimo principas labai paprastas: visas duomenų masyvas yra „skenuojamas“ ir ieškoma pačio mažiausio elemento, tada tas elementas yra nukeliamas į masyvo pradžią (jeigu reikia, kad duomenys būtų surikiuoti nuo mažiausio iki didžiausio). Vėliau ciklas kartojamas, tik šįkart netikrinant pirmojo masyvo elemento. Iš krūvos likusių elementų yra išrenkamas mažiausias ir jis jau yra statomas į antrąją masyvo vietą. Vieno ciklo („skenavimo“) metu gali būti perkeliamas tik vienas elementas, todėl šis algoritmas yra ganėtinai lėtas, jeigu duomenų kiekiai yra dideli. Manau iš iliustracijos suprasti bus šiek tiek lengviau.
Šis metodas vėliau buvo patobulintas ir pavadintas „Double selection sort“ (dvigubo išrinkimo algoritmas). Šio metodo principas yra lygiai tas pat, tik „skenuojant“ masyvą yra ieškoma ne tik mažiausių elementų, bet ir didžiausių ir vėliau mažiausias elementas nukeliamas į masyvo pradžią, didžiausias – į pabaigą. Vėliau procesas kartojamas, tik į jį neįtraukiamas pirmasis ir paskutinis masyvo elementai. Toks mažytis patobulinimas leido šį algoritmą pagreitinti du kartus. Internete neradau geros iliustracijos pavaizdavimui, tačiau manau nėra sunku įsivaizduot tokį procesą, jeigu pilnai supratote „Selection sort“.
Trečias metodas, apie kurį noriu papasakoti yra „Insertion sort“ (įterpimo algoritmas). Šis algoritmas nėra labai dažnai sutinkamas ir aš pats jo beveik niekad nenaudoju, tačiau jo veikimo principas nėra labai sunkiai suprantamas. Šio metodo metu masyvas yra suskaidomas į dvi dalis – surūšiuotąją dalį ir nesurūšiuotą dalį. Surūšiuota masyvo dalis būna masyvo pradžioje, nesurūšiuota – pabaigoje. Kiekvienos iteracijos (ciklo) metu, imamas vienas iš nesurūšiuotos dalies elementų (paprastai visi elementai imami paeiliui) ir to elemento reikšmė yra išsaugoma kintamajame ir iš masyvo ištrinama (paliekama tuščia vieta). Vėliau tikrinama, į kurią surūšiuotos masyvo vietos dalį tas elementas turėtų tikti, t.y. jeigu prieš tai buvęs elementas yra mažesnis už pasirinktąjį, o kitas yra didesnis, reiškia šioje vietoje reikia įterpti tą elementą. Pvz. turime surūšiuotą masyvo dalį [1][3][4][5] ir turime elementą [2], pradedame nuo surūšiuoto masyvo galo tikrinti, kur tas [2] turėtų tikti – pirma tikriname [4][5], kadangi [4] yra didesnis už [2], tai jo vieta yra ne čia. Vėliau tikriname [3][4], kadangi, vėlgi, [3] yra daugiau nei [2], čia šis elementas netinka, tęsiame procesą su [1][3]. Kadangi 1 yra mažiau už [2] ir [3] yra daugiau už [2], tai šioje vietoje reikia įterpti šį elementą. Elementas [2] yra įterpiamas į antrą masyvo poziciją, tuo tarpu [3][4][5] yra perstumiami viena pozicija toliau. Nemoku puikiai paaiškinti šių dalykų teksto forma, todėl iš iliustracijos manau susigaudyti bus daug paprasčiau.
Ketvirtas, šiek tiek primenantis „Insertion sort“ (bent man) yra vadinamas „Bubble sort“ (Burbulo algoritmas). Šį algoritmą suprast ir sugebėt pritaikyt turėtų mokėt kiekvienas pradedantis programuotojas. Suprast šį metodą yra labai nesunku, sudėtingiau šiek tiek yra jį panaudoti praktikoje. Burbulo algoritmas yra pakankamai lėtas, tačiau jo pagrindinis privalumas yra tas, kad jis nenaudoja kompiuterio atminties – nereikia nustatyti jokių papildomų kintamųjų, užtenka turėt tik patį masyvą. Veikimo principas yra toks: pradedama yra nuo masyvo pabaigos, yra imami du masyvo elementai ir jie kartu yra lyginami. Jeigu antrasis elementas yra mažesnis už pirmąjį – jie yra apkeičiami vietomis ir mažesnis elementas pakliūva arčiau masyvo pradžios. Po šio apkeitimo yra imami kiti du elementai (priešpaskutinis masyvo elementas ir elementas, esantis jam iš kairės) ir jie identiškai yra tikrinami – jeigu antrasis elementas yra mažesnis už pirmąjį – jie yra apkeičiami vietomis, jeigu visgi antrasis elementas yra didesnis už pirmąjį nedaroma nieko ir pereinama prie kitų dviejų elementų. Pavyzdys: tarkim turime masyvą iš trijų elementų [4][1][3]. Pirma paimame du paskutinius masyvo elementus [1] ir [3]. Kadangi [1] yra mažesnis už [3], nieko su jais nedarome. Einame prie kitų dviejų elementų – [4] ir [1]. Kadangi kairysis elementas ([4]) yra didesnis už dešinįjį, apkeičiame juos vietomis ir gauname masyvą [1][4][3]. Baigėsi viena ciklo iteracija. Vėl visą procesą kartojame iš naujo – tikriname paskutinius du elementus [4][3], kadangi [4] daugiau už [3], apkeičiame juos vietomis, vėliau imant [1][3] nereikės nieko keisti vietomis. Galiausiai turime surikiuotą masyvą – [1][3][4]. Iliustracijoje pavaizduotas tas pat algoritmas tikrinant masyvą nuo jo pradžios. Praktiškai nėra jokio skirtumo, ar masyvas bus pradėtas rūšiuoti nuo pradžios, ar nuo pabaigos. Jeigu bus pradedama rūšiuoti nuo pradžios, pirmiausia bus surūšiuoti didžiausi masyvo elementai, jeigu bus pradedama rūšiuoti nuo pabaigos – pirmiausia bus surūšiuojami mažiausi masyvo elementai.
Na ir paskutinis, kurį aptarsiu šiame straipsnyje, yra „Quicksort“ algoritmas. Lietuviškai jis skambėtų kaip „greitojo rikiavimo algoritmas“, tačiau retai jis taip vadinamas. Tai vienas iš greičiausių ir plačiausiai naudojamų algoritmų. Mano aukščiau minėti algoritmai visi turėjo vieną pagrindinę neigiamą savybę – jie veikia pernelyg lėtai, kai masyvas yra didelis (rikiuojama labai daug duomenų), tuo tarpu „Quicksort“ lengviau tvarkosi su didesniais duomenų kiekiais negu su mažesniais. Būtent dėl šios priežasties šis algoritmas yra plačiai paplitęs. „Quicksort“ veikimo principas yra toks: pirma yra paimamas vienas iš masyvo elementų (geriausia, kad tas elementas būtų mediana, tačiau praktikoje tai neefektyvu, nes tam reikia skenuot visą masyvą ir tokiu būdu nustatyti medianą). Vėliau visas masyvas yra suskaidomas yra dvi dalis – pirmojoje dalyje yra visi masyvo elementai, kurie yra didesni už paimtą skaičių, antroje – mažesni. Tas skaičius, kuris buvo paimtas, yra vadinamas „Pivot“ ir po šio perrinkimo galime garantuoti, kad šis skaičius tikrai yra savoje vietoje. Vėliau šis procesas kartojamas paėmus jau kitą „pivot“ skaičių vienoje iš likusių dviejų masyvo dalių. Realiai, tokiu būdu masyvas yra suskaidomas į kelias dalis, kurios vėliau rūšiuojamos atskirai. Šio dalyko pliusas yra tas, kad kai kuriais atvejais vienos iteracijos metu gali būti surūšiuojami keli elementai, tuo tarpu visuose ankstesniuose algoritmuose per vieną iteraciją savo vietą masyve atrasdavo tik vienas elementas. Tai „Quicksort‘ui“ leidžia didelius masyvus surūšiuoti daug greičiau. Šio rūšiavimo pavyzdys: tarkime turime masyvą [1][5][9][3][7][8][4], paimame vieną atsitiktinį „pivot“ skaičių, tarkime tas skaičius yra [5], tada visus mažesnius elementus stumiame į kairę, didesnius – į dešinę pusę ir gauname tokį masyvą: [1][3][4][5][9][7][8], po šio perrikiavimo [5] dabar tikrai yra savoje vietoje. Dabar imame bet kurį atsiktinį skaičių iš „mažesniojo“ masyvo, tarkime tai bus [1], po perrikiavimo gauname tokį masyvą – [1][3][4][5][9][7][8], [1] dabar tikrai yra savo vietoje. Dabar imame vieną iš likusių dviejų skaičių [3] arba [4] atsitiktinai ir po patikrinimo gausime [1][3][4][5][9][7][8]. Kaip matome per tris iteracijas sugebėjome surikiuoti keturis elementus. Dabar lieka kitas, mažesnis masyvas – tarkime atsitiktinai išrenkamas skaičius [8], tai po šios iteracijos visas masyvas bus surikiuotas – [1][3][4][5][7][8][9]. Kadangi po perrinkimo tarpuose liko po vieną skaičių – [7] ir [9], tai tų skaičių nėra su kuo lyginti, o tai reiškia, kad jie tikrai yra savose vietose. Kaip matome, užteko vos 4-ių iteracijų, kad surikiuotume 7-ių elementų masyvą!
Kurį metodą kada naudoti? Na, tai priklauso nuo turimo masyvo dydžio ir nuo to, kokie duomenys jame saugomi. Realiai didelio skirtumo tarp visų šių metodų nėra, jeigu masyvas yra nedidelis (tarkim iki 500 elementų), kai kuriais atvejais, dirbant su nedideliais masyvais, koks įterpimo algoritmas surikiuoja duomenis greičiau negu „Quicksort‘as“. Kalbant apie masyvus, kuriuose yra saugomi kažkokie ilgi teksto blokai ir elementų kiekis nėra didelis, naudinga būtų naudoti „Bubble sort“ metodą dėl to, nes jis nenaudoja operatyviosios atminties (nereikia kelti didelių duomenų į RAM, vėliau atlaisvinti RAM ir vėl kelti naujus, kas gali kainuoti kelias milisekundes). Kalbant apie didelius masyvus, kuriuose yra tūkstančiai elementų, aiškus lyderis čia yra „Quicksort“ dėl savo galimybės greitai dirbti su dideliais masyvais. Na, aišku, jeigu turite milijonus ar milijardus nerūšiuotų elementų, tokiu atveju net ir „Quicksort“ darbuosis ilgą laiką.
Pabaigai dar norėčiau pridurti, kad pradinėje straipsnio versijoje buvau įdėjęs ir kodo pavyzdžių, tačiau pamačiau, kad juos įdėjus straipsnio apimtys beveik padvigubėja (o jis ir taip nėra trumpas), tuo tarpu įvedus į „Google“ ar „Bing“ vien algoritmo pavadinimą, yra labai nesunku rasti bent keletą kodo pavyzdžių (paprastai pirmajame, dažniausiai „Wikipedijos“, rezultate jau būna pateikta bent pora kodo pavyzdžių – C++ ir Pascal kalbomis). Taip pat pranešu, kad laikinai išjungiau komentavimo tinklaraštyje galimybę, nes užpuolė šiandien spambotai – daugiau negu 1000 komentarų teko šiandien ištrinti. Kai tik surasiu sprendimą, kaip atsikratyti šių viagros pardavėjų, iškart vėl įjungsiu komentavimo galimybę. Jeigu kas nors žinote, kaip būtų galima tai sutvarkyti, būčiau dėkingas jei praneštumėte apie tai, mano kontaktus galima rasti “Kontaktai” skiltyje. Dėkoju ir atsiprašau už nepatogumus.

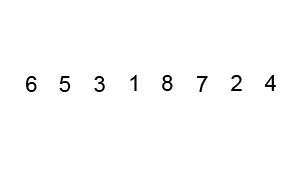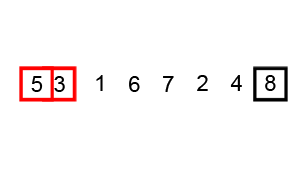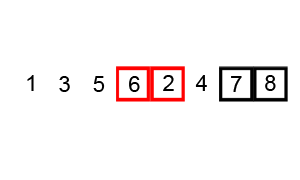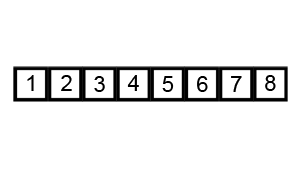




Ypatingai domino quicksort’as Ačiū
Ačiū